Mé konzultační hodiny v září
- Vzhledem k tomu, že poslední zkouškový termín je středa 23.9., přijímám zápočtové programy (a náhradní domácí úlohy) do středy 16.9 (23:59).
- pondělí 13:00 - 15:00
- čtvrtek 9:00 - 11:00
- pouze po předchozí domluvě emailem!
- Od úterý 8.9. do pátku 11.9. budu mimo Prahu a email.
- Od soboty 19.9. budu mimo Prahu a email. Zápočtové úlohy, které mi pošlete po tomto termínu, si už stoprocentně neprohlédnu.
Mé konzultační hodiny ve zkouškovém období (červen)
- úterý 9:00 - 11:00
- čtvrtek 13:00 - 15:00
- pouze po předchozí domluvě emailem!
- během července a srpna konzultace po domluvě emailem (počítejte s delší dobou odezvy)
Náhradní domácí úkoly
- Studenti, kteří během semestru nezískali za žádný testík více než 3 body a chtějí ode mě zápočet, musí za dostatečně bodů napsat náhradní testík (z Haskellu nebo Prologu - podle vlastních preferencí), počet pokusů je "neomezený".
- Nezapomeňte, že povinná je účast na 9 cvičeních, kdo chyběl vícekrát, musí účasti dorovnat z bodů za domácí úkoly nebo testíky (v poměru 2:1). Naopak, kdo má více než 9 účastí, může přebytečné účasti převést na body za domácí úkoly v poměru 1:2.
- Studenti, kteří během semestru nezískali dostatek bodů za domácí úkoly a chtějí ode mě zápočet, mohou vypracovat náhradní úlohy, aby body dorovnali.
- Studenti, kterým chybí (po případném převedení bodů za testíky) více než 8 bodů, si zvolí náhradní úlohu (z Haskellu nebo Prologu) rozsahu (menšího) zápočtového programu. Na tématu se můžeme domluvit emailem.
- Studenti, kterým chybí maximálně 8 bodů, si mohou vybírat také z následujících náhradních úloh (podrobnější zadání úloh v případě zájmu doplním).
- Náhradní domácí úkoly z Haskellu (náhrada za některé úkoly ze cvičení 9-11)
- Řídká matice je reprezentována jako trojice (m,n,s), kde m je počet řádek, n je počet sloupců a s je seznam trojic (i,j, a_ij), kde i je číslo řádky, j je číslo sloupce a a_ij je nenulová hodnota. Seznam trojic je přitom uspořádaný vzestupně podle i a uvnitř řádek pomocí j. Definujte funkce, které v této reprezentaci realizují:
- matice a) (za 0,5 bodu) transpozici matic
- matice b) (za 1 bod) násobení matic
- matice c) (za 1 bod) "chytré" (efektivní) umocňování matic
- Náhradní domácí úkoly ze SCHEME (náhrada za některé úkoly ze Scheme ze cvičení 7-8)
- Navrhněte vhodnou reprezentaci prostorového závěsného mobilu ve SCHEME (co je prostorový mobil, jsme definovali na cvičení). Definujte funkce, které v této reprezentaci realizují:
- mobil a) (za 0,5 bodu) test, zda je mobil vyvážený
- mobil b) (za 1 bod) vyvážení prostorového mobilu
- mobil c) (za 1,5 bodu) test, zda (vyvážený) mobil "cinká" (tj. zda se dráhy některých ramen při otáčení protínají), případně vhodným způsobem vrátit i pozice, kde mobil cinká
- Náhradní domácí úkoly z PROLOGU (náhrada za některé úkoly z Prologu)
- Úlohy z 6-tého domácího úkolu které jste neodevzdali - nthPerm (1 bod), vyhodnot (0,5 bodu), vyhodnot1 (0,5 bodu), tautologie (1 bod)
- Symbolické derivování a zjednodušování výsledných výrazů (podle obtížnosti až 4 body).
11. domácí úkol 14.5.2009
- HASKELL
- Do příště
- Ti z Vás, kterým se nepovedla žádná / některá z písemek za více než 3 body (nebo ji vůbec nepsali), si mohou na posledním cvičení napsat opravu (varianty budou - Prolog - Prolog+SCHEME - Haskell).
- a) (za 1 bod) Navrhněte v Haskellu Pascalův trojúhelník jako nekonečnou datovou strukturu - definujte funkci pascal, která Pascalův trojúhelník vytvoří.
- b) (za 1 bod) Uvažujme binární vyhledávací strom definovaný pomocí:
data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Eq)
v jehož uzlech je uložena informace nějakého typu (podtřídy Ord). Definujte funkci delete x a, která z binárního vyhledávacího stromu x vypustí uzel s hodnotou a (není-li tam, bude to identita). - b) (za 1,5 bodu) Uvažujme binární vyhledávací strom definovaný pomocí:
data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Eq)
v jehož uzlech je uložena informace nějakého typu (podtřídy Ord). Definujte funkci deleteRange x a b, která z binárního vyhledávacího stromu x vypustí uzly patřící do zadaného intervalu [a,b] (nejsou-li tam žádné, bude to identita).
10. domácí úkol 7.5.2009
- HASKELL
- Příště budeme psát testík z Haskellu.
- Domácí úkoly d), e), f) z minule.
- Do příště (bonusové domácí úkoly pro ty, kteří mají zatím málo bodů za domácí úkoly)
- a) (za 1 bod) Definujte funkci del x, která vrátí seznam dělitelů (celého nezáporného) čísla x.
- b) (za 0,75 bodu) Definujte funkci prv n, která testuje, zda n je prvočíslo.
- c) (za 0,75 bodu) Definujte funkci delmoc x d, která vrátí maximální mocninu čísla d, která dělí x (např. (delmoc 100000 100) == 2).
- d) (za 1,5 bodu) Napište funkci qsum a b c analogickou následujícímu for-cyklu v jazyku C:
s=0; for (i = A; C(i) < B(i); i++) s += C(i);- Kde A, B, C jsou parametry - A je číslo, B a C jsou funkce jedné proměnné, to budou také parametry požadované funkce qsum. Cílem je tedy spočítat součet hodnot C(A), C(A+1), C(A+2), C(A+3), ..., C(A+j), kde j je maximální takové, že C(A+j) < B(A+j).
- Nápověda: foldl, takeWhile
9. domácí úkol 30.4.2009
- HASKELL
- 0. Nainstalujte si interpret Haskellu a vyzkoušejte si práci v něm.
- Do příště
- a) (za 0,5 bodu) Definujte funkci, která spočte součet všech prvků seznamu celých čísel.
- b) (za 0,5 bodu) Definujte funkci, která spočte součin všech prvků seznamu celých čísel.
- c) (za 1 bod) Definujte funkci, která vytvoří seznam obsahující prvních n členů aritmetické posloupnosti (a_i = a_0 + d * i).
- Nezapomeňte na (správnou) definici typů!
- Stačí za 14 dnů:
- d) (za 1 bod) Definujte funkci, která vytvoří nekonečný seznam obsahující aritmetickou posloupnost (ta je definovaná předpisem a_i = a_0 + d * i).
- f) (za 1,5 bodu) Definujte funkci, která vytvoří nekonečný seznam.
Posloupnost je dána následujícím rekurentním předpisem:
a_0 = 1
a_1 = 2
a_2 = 3
a_[n+1] = 3*a_n + 2*a_[n-1] + a_[n-2]
- e) (za 1,5 bodu) Definujte funkci, která vytvoří nekonečný seznam.
Posloupnost je dána následujícím rekurentním předpisem:
a_0 = 3
a_1 = 2
a_2 = 1
a_n = a_0 + a_1 + ... + a_[n-1]
8. domácí úkol 23.4.2009
- SCHEME
- a) (za 1 bod) Na cvičení jsme definovali funkci map pro seznamy. Napište funkci (mapTree t f) , která je analogií funkce map, ale na vstupu má na místo seznamu binární strom t a funkci f. Funkce mapTree aplikuje funkci f na každý vnitřní uzel stromu (tj. na jeho hodnotu) a vrátí výsledný strom.
- b) (za 1 bod) Na cvičení jsme definovali funkci app pro seznamy. Napište funkci (appTree t f g) , která je analogií funkce app, ale na vstupu má na místo seznamu binární strom. Funkce appTree aplikuje funkci g (s jedním parametrem) na listy stromu a funkci f (se třemi parametry) rekurzivně na vnitřní uzly stromu (parametry f jsou hodnota uzlu, "to, co přišlo zleva" a "to, co přišlo zprava").
- c) (za 1 bod) Napište dvě z následujících funkcí za využití appTree nebo mapTree: sumTree (součet prvků ve stromě), countTree (počet prvků ve stromě), minTree (minimální prvek ve stromě), dvakrat (vrací strom, kde budou všechny prvky vynásobené dvěma), nadruhou (vrací strom, kde budou všechny prvky umocněné nadruhou). Už si nepamatuji, které z těchto nebo podobných funkcí jsem zadala za domácí úkol na cvičení, proto dávám nyní na výběr :-).
7. domácí úkol 16.4.2009
- PROLOG Zadání z minule - vyhodnocování booleovských výrazů
- Do příště byste si měli vybrat téma zápočtového programu. Poté, co se na tématu dohodneme, mi pošlete specifikaci (podrobnější zadání) programu. Termín na odeslání specifikace je 30.duben.
- Příště budeme psát testík (příklady z Prologu a základů Lispu). Pokud zvládnete dnešní domácí úkoly, neměl by pro vás ani testík být problém :).
- SCHEME
- a) (za 0,5 bodu) Napište funkci minimumS , která má na vstupu seznam čísel a vrátí minimální číslo ze seznamu.
- b) (za 0,5 bodu) Napište funkci deleteS , která má dva parametry - seznam čísel a prvek seznamu. Funkce vrátí seznam bez prvního výskytu prvku.
- c) (za 0,5 bodu) Napište funkci minSort , která má jeden parametr - seznam čísel (čísla se v něm mohou opakovat). Funkce vrátí vzestupně setříděný seznam. Implementuje třídění přímým výběrem minima.
- d) (za 0,5 bodu) Napište funkci zatridS , která má dva parametry - vzestupně setříděný seznam čísel (čísla se mohou opakovat) a číslo. Funkce vrátí seznam, který vznikne zařazaním čísla na správné místo do seznamu.
- e) (za 0,5 bodu) Napište funkci insertSort , která má jeden parametr - seznam čísel (čísla se v něm mohou opakovat). Funkce vrátí vzestupně setříděný seznam. Implementuje třídění vkládáním (postupným zatřizováním prvků).
6. domácí úkol 9.4.2009
- Úkol c) z minule (až za 1,5 bodu) (do příště). Definujte predikát nthPerm(+N,?K,?P), kde P je K-tá permutace čísel {1,2,...,N} podle lexikografického uspořádání (P je seznam). Predikát by měl fungovat oběma směry: pro K najít K-tou permutaci, pro permutaci P zjistit, kolikátá je.
- Na cvičení jsme si řekli principy, jak se dá spočítat K-tá permutace seznamu a jak se naopak zjistí pořadí permutace - oboje v čase O(N^2). Můžete je použít :-). Každopádně, zvýšenou pozornost věnujte časové a prostorové složitosti použitého algoritmu - neměla by být vyšší než O(N^2).
- Rada: Na cvičení jsme si také říkali, jak ošetřit, aby šel predikát použít oběma směry (nthPerm(+N,+K,-P), nthPerm(+N,-K,+P)) - pomocí predikátů var / nonvar a pomocí zvláštní procedury pro každý směr.
- Vyhodnocování booleovských výrazů
- Tento domácí úkol stačí odevzdat za 14 dnů, tj. před cvičením 23.4.2009.
- a) (za 1 bod) Úkolem je vyhodnotit zadaný booleovský výraz sestavený z booleovských konstant true a false, z logických spojek (not, and, or, implikace, ekvivalence) a závorek. Logickým spojkám přitom odpovídají následující operátory: - (NOT), * (AND), + (OR), -> (implikace), <-> (ekvivalence). Tedy term true*(false+ -true) odpovídá formuli TRUE AND (FALSE OR NOT TRUE).
Spojky definujte jako operátory např takto:
:- op(200, fy, -). % NOT
:- op(210, yfx, *). % AND
:- op(220, yfx, +). % OR
:- op(230, xfy, ->). % IMPLIKACE
:- op(240, xfx, <->).% EKVIVALENCE
% :- op(260, xfy, :) % do zadání b)
Definujte predikát vyhodnot(+Vyraz,-Hodnota), kde Hodnota je pravdivostní hodnota booleovského výrazu Výraz.
Například: ?- vyhodnot((-false)*(true+false),H). H = true. - Drobná nápověda, jak na to (pro negaci):
vyhodnot(-B,V):- vyhodnot(B,V1), negace(V1,V). % rekurze a vyhodnocení spojky
% negace - definice výčtem:
negace(true, false).
negace(false, true).
- b) (za 1,5 bodu) Rozšiřte definici booleovského výrazu o proměnné a definujte predikát vyhodnot1(+Vyraz,+TabulkaProměnných, -Hodnota), kde Hodnota je pravdivostní hodnota booleovského Vyrazu pro pravdivostní hodnoty proměnných, které jsou uloženy v seznamu TabulkaProm. Proměnné jsou reprezentovány atomy (ruznými od true a false). TabulkaProměnných je seznam termů ve tvaru proměnná:true nebo proměnná:false. Například: vyhodnot1((-x)*(x+y),[x:false,y:true,z:true],H) H = true.
- c) (za 1 bod) Definuje predikát tautologie(+Vyraz), kde výraz Vyraz je tautologií (nabývá hodnoty pravda pro všechny možné pravdivostní hodnoty svých proměnných).
- Příklady dotazů a (snad :) ) správných odpovědí:
?- vyhodnot(true,V).
V=true.
?- vyhodnot(false,V).
V=false.
?- vyhodnot(-true,V).
V=false.
?- vyhodnot(true*(-false),V).
V=true.
?- vyhodnot((-true)+(-false),V).
V=true.
?- vyhodnot(false->true,V).
V=true.
?- vyhodnot(-(false*true),V).
V=true.
?- vyhodnot((false*(-true))<->(true -> false),V).
V=true.
?- vyhodnot((true*(false -> true))<->(true -> false),V).
V=false.
?- vyhodnot1(false,[],V).
V=false.
?- vyhodnot1(x,[x:true],V).
V=true.
?- vyhodnot1(x,[x:false],V).
V=false.
?- vyhodnot1(x + y,[x:false, y:true],V).
V=true.
?- vyhodnot1(x -> (y -> -x),[x:false, y:true],V).
V=true.
?- vyhodnot1(( -x + y) <-> -(-y * -x),[x:true, y:true],V).
V=true.
?- vyhodnot1(x* -y*z* -a* -b,[a:false,x:true,y:false,z:true,b:false],V).
V=true.
?- tautologie(true).
yes
?- tautologie(false).
no
?- tautologie(x -> true).
yes
?- tautologie(x + -x).
yes
?- tautologie(x * -x).
no
?- tautologie(x -> (y -> x) ).
yes
?- tautologie((-x -> -y) <-> (y -> x) ).
yes
5. domácí úkol 2.4.2009
- V tomto domácím úkolu věnujte zvýšenou pozornost časové složitosti použitého algoritu a eleganci řešení.
- a) (za 1 bod) Na vstupu máme matici M. Definujte predikát pecka(+M,?Pecka,?Slupka), ketrý matici M rozdělí na "vnitřek" (Pecka) a "obal" (Slupka). Slupka je matice M, kde je "vnitřek" vyplněn nulami. Snažte se nalézt elegantní řešení.
- b) (za 1 bod) Na vstupu máme seznam S, který reprezentuje permutaci množiny přirozených čísel {1,2,...,n}. Definujte predikát nextPerm(+S,-NS), který k S vrátí lexikograficky následující permutaci.
- c) (za 0,5-1,5 bodu podle časové složitosti algoritmu) Definujte predikát nthPerm(+N,?K,?P), kde P je K-tá permutace čísel {1,2,...,N} podle lexikografického uspořádání (P je seznam). Predikát by měl fungovat oběma směry: pro K najít K-tou permutaci, pro permutaci P zjistit, kolikátá je.
- Rada: Vzpomeňte si (při řešení b a c) na probrané vestavěné predikáty var, nonvar,...
- Příklady dotazů a správných odpovědí:
?- pecka([[1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1],[1, 1, 1, 1, 1, 1],[1, 1, 1, 1, 1, 1],[1, 1, 1, 1, 1, 1]],[[1, 1, 1, 1],[1, 1, 1, 1],[1, 1, 1, 1]], [[1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 1], [1, 0, 0, 0, 0, 1], [1, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1]]).
true.
?- pecka([[3, 0, 4, 2, 1, 0], [1, 3, 2, 0, 1, 1], [4, 4, 5, 5, 3, 3]], Pecka, Slupka). Pecka = [3, 2, 0, 1], Slupka = [[3, 0, 4, 2, 1, 0], [1, 0, 0, 0, 0, 1], [4, 4, 5, 5, 3, 3]]
?- pecka([[3, 3, 4, 2, 1, 0], [1, 3, 2, 5, 1, 1]], Pecka, Slupka). Pecka = [], Slupka = [[3, 3, 4, 2, 1, 0], [1, 3, 2, 5, 1, 1]]
?- nextPerm([2,3,1,4], P).
P = [2,3,4,1]
?- nextPerm([4,5,3,2,1], P).
P = [5,1,2,3,4]
?- nextPerm([5,4,3,2,1], P).
no. % nebo P = [1,2,3,4,5]
?- nthPerm(5,1,P).
P = [1,2,3,4,5]
?- nthPerm(5,K,[1,5,2,4,3]).
K = 20
?- nthPerm(_,K,[4,1,3,2]).
K = 20
?- nthPerm(6,K,[1,2,3,4,5]).
no.
4. domácí úkol 26.3.2009
- a) (za 1,5 bodu) Na vstupu máme seznam S. Definujte predikát multijoin(+S,?T), kde seznam T je "multisjednocením" seznamu S. Multisjednocením se rozumí odstranění všech hranatých závorek, tedy obsahuje-li seznam prvek, který je také seznam, tak je nahrazen prvky tohoto seznamu, například z [1,[2,[],3,[4]],5] se nahrazením získá seznam [1,2,3,4,5].
- b) (za 2 body) Na vstupu máme dvě matice A a B. Definujte predikát vynasob(+A,+B,-M), který implementuje násobení matic. Matice jsou reprezentovany jako seznamy řádků. Predikát by měl odpovědět no pro matice, které nelze navzájem vynásobit (za nesplnění této podmínky bude "sankce" 0.5 bodu).
- Rada - při definici predikátů se můžete inspirovat predikáty definovnými na cvičeních (popř. se vám některé mohou hodit): např. multijoin2(+S,-T), aj.
- Příklady dotazů a správných odpovědí:
?- vynasob([[2, 3], [1, 4]],[[-1, 2], [1, -2]], M).
M = [[1, -2], [3, -6]]
?- vynasob([[2,3,1], [1,4,1]],[[-1, 2, 1], [1, -2, 0]], M).
no
?- multijoin([[[a]],1,2,[a,[b,[]]]],S).
S = [a,1,2,a,b]
3. domácí úkol 19.3.2009
- POZOR! Na příštím cvičení budeme psát test!
- Pokračování příkladu ze cvičení - viz. predikát prostredni/2 řešený trikem. Bez použití aritmetiky (predikát is) definujte následující predikáty:
- Pro zadání c) a d) uvažujeme seznamy pouze osob (mužů a žen), muži jsou definovaní pomocí predikátu muz/1, ženy pomocí predikátu zena/1.
- a) (za 0.5 bodu) napoloviny(+S,-T1,-T2), seznam S je zřetězením seznamů T1 a T2, přičemž počet prvků v T1 a v T2 se liší nejvýše o 1
- b) (za 0.5 bodu) natretiny(+S,-T1,-T2,-T3), seznam S je zřetězením seznamů T1, T2 a T3, přičemž počet prvků v libovolných dvou ze seznamů T1, T2 a T3 se liší nejvýše o 1
- c) (za 1 bod) polovinymuzu(+S,-T1,-T2), seznam S je zřetězením seznamů T1 a T2, přičemž počet mužů v T1 a v T2 se liší nejvýše o 1 (na počtu žen v T1, T2 nezáleží)
- d) (za 1 bod) tretinymuzu(+S,-T1,-T2,-T3), seznam S je zřetězením seznamů T1, T2 a T3, přičemž počet mužů v libovolných dvou ze seznamů T1,T2 a T3 se liší nejvýše o 1 (na počtu žen v T1, T2, a T3 nezáleží)
% muz(X)
muz(karel).
muz(tomas).
muz(lukas).
muz(david).
muz(pavel).
muz(milan).
muz(simon).
muz(jirka).
muz(quido).
muz(vojta).
% zena(X)
zena(pavla).
zena(verka).
zena(petra).
zena(marta).
zena(klara).
zena(zdena).
zena(hanka).
?- napoloviny([a,b,c,d,e,f],A,B).
A = [a,b,c] ,
B = [d,e,f] ;
no
?- napoloviny([a,b,c,d,e,f,g,h,i],A,B).
A = [a,b,c,d,e] ,
B = [f,g,h,i] ;
no
?- napoloviny([a],A,B).
A = [a] ,
B = [] ;
no
?- natretiny([a,b,c,d,e,f],A,B,C).
A = [a,b] ,
B = [c,d] ,
C = [e,f] ;
no
?- natretiny([a,b,c,d,e,f,g],A,B,C).
A = [a,b,c] ,
B = [d,e] ,
C = [f,g] ;
no
?- polovinymuzu([karel,tomas,lukas,david,pavel,jirka,quido,vojta,simon,milan],A,B).
A = [karel,tomas,lukas,david,pavel] ,
B = [jirka,quido,vojta,simon,milan] ;
no
?- polovinymuzu([pavla,karel,verka,petra,tomas,zdena],A,B).
A = [pavla,karel] ,
B = [verka,petra,tomas,zdena] ;
no
?- tretinymuzu([karel,tomas,lukas,david,pavel,jirka,quido,vojta,simon,milan],A,B,C).
A = [karel,tomas,lukas,david] ,
B = [pavel,jirka,quido] ,
C = [vojta,simon,milan] ;
no
?- tretinymuzu([pavla,karel,verka,petra,tomas,lukas,david,marta,pavel,jirka,klara,quido,vojta,simon,milan,zdena],A,B,C).
A = [pavla,karel,verka,petra,tomas,lukas,david] ,
B = [marta,pavel,jirka,klara,quido] ,
C = [vojta,simon,milan,zdena] ;
no
2. domácí úkol 12.3.2009
- a) Pokračování příkladu ze cvičení - modelování přirozených čísel pomocí termů 0, s(0), s(s(0)),...
- a1) (za 0.5 bodu) Definujte predikát mod(+X,+Y,?Z), tak že Z = X mod Y (X,Y,Z jsou přirozená čísla modelovaná pomocí termů)
- a2) (za 0.5 bodu) Definujte predikát fact(+X,?F), tak že F = X! (X, F jsou přirozená čísla modelovaná pomocí termů)
- Rada - při definici predikátů můžete použít predikáty definovné na cvičení: natural(X), add(X,Y,Z), mul(X,Y,Z) aj.
- Příklady dotazů a správných odpovědí
?- mod(s(s(s(s(s(s(s(0))))))),s(s(s(s(0)))),X).
X = s(s(s(0))) .
?- mod(s(s(s(s(s(s(s(0))))))), s(s(0)),X).
X = s(0) .
?- fact(s(s(s(0))),F).
F = s(s(s(s(s(s(0)))))) ;
no
?- fact(s(s(s(s(0)))),F).
F = s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(s(0)))))))))))))))))))))))) ;
no
- b) Příklad na rodinné vztahy.
- Uvažujeme databázi faktů muz(X), zena(X), rodina(Otec, Matka, Seznam dětí od nejstaršího k nejmladšímu).
- b1) (za 0.5 bodu) Definujte predikát mladsisestra(?Ci,?MladsiSestra).
- b2) (za 0.5 bodu) Definujte predikát starsibratr(?Ci,?StarsiBratr).
- b3) (za 1 bod) Definujte predikát nejmladsisestra(?Ci,?NejmladsiSestra).
- b4) (za 1 bod) Definujte predikát nejstarsibratr(?Ci,?NejstarsiBratr).
- Pozor! - nejmladší sestra Ci nemusí být mladší než Ci, stejně tak nejstarší bratr Ci nemusí být starší než Ci.
- Rada - při definici predikátů se vám mohou (ale nemusí) hodit pomocné predikáty: mladsi(SeznamSourozencu, StarsiSourozenec,MladsiSourozenec), vypust(+Seznam,+Prvek,-VyslednySeznam)
- Příklad databáze faktů:
% rodina(Otec,Matka, Seznam deti od nejstarsiho k nejmladsimu)
rodina(borivoj, anna, [jana, petr, pavel,pavla,vera,marcela,jan]).
rodina(simon,marcela,[]).
rodina(pavel,klara,[zdena]).
rodina(petr,bozena,[tomas]).
rodina(pavel,bozena,[lukas,david]).
rodina(tomas,pavla,[verka,dan]).
rodina(david,verka,[karel,petra]).
% muz(X)
muz(borivoj).
muz(dan).
muz(karel).
muz(tomas).
muz(lukas).
muz(david).
muz(petr).
muz(pavel).
muz(jan).
muz(simon).
% zena(X)
zena(pavla).
zena(vera).
zena(marcela).
zena(jana).
zena(anna).
zena(klara).
zena(zdena).
zena(bozena).
zena(verka).
zena(petra).
- Příklady dotazů a správných odpovědí pro naše fakta: (pořadí odpovědí se může lišit)
?- starsibratr(marcela,B).
B = petr ;
B = pavel ;
no
?- starsibratr(lukas,B).
no
?- starsibratr(Ci,pavel).
Ci = pavla ;
Ci = vera ;
Ci = marcela ;
Ci = jan ;
no
?- mladsisestra(karel,S).
S = petra ;
no
?- mladsisestra(Ci,vera).
Ci = jana ;
Ci = petr ;
Ci = pavel ;
Ci = pavla ;
no
?- nejmladsisestra(Ci,verka).
Ci = dan ;
no
?- nejmladsisestra(petra,S).
no
?- nejmladsisestra(Ci,marcela).
Ci = jana ;
Ci = petr ;
Ci = pavel ;
Ci = pavla ;
Ci = vera ;
Ci = jan ;
no
?- nejstarsibratr(jana,B).
B = petr ;
no
?- nejstarsibratr(petr,B).
B = pavel ;
no
1. domácí úkol 5.3.2009
- a) Vyzkoušejte si práci se zvoleným interpretem Prologu, například SWI-Prolog
- b)(za max. 1 bod) Pokračování příkladu ze cvičení. Definujte predikát cesta(+Od,?Do,?Cesta)
- Uvažujeme graf popsaný fakty hrana(Od,Do), například:
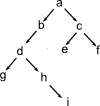
- Na cvičení jsme definovali rekurzivni predikát cesta(Od,Do).
- Definujte podobný predikát cesta(+Od,?Do,?Cesta), který navíc vypíše seznam vrcholů po cestě.
- Fakta popisující obrázek:
hrana(a,b).
hrana(b,d).
hrana(d,g).
hrana(d,h).
hrana(h,i).
hrana(a,c).
hrana(c,e).
hrana(c,f).
- Příklady dotazů a správných odpovědí pro naše fakta:
?- cesta(d,h,S).
S = [d,h];
no
?- cesta(f,X,S).
no
?- cesta(a,a,S).
no
?- cesta(b,X,S).
X = d , S = [b,d] ;
X = g , S = [b,d,g] ;
X = h , S = [b,d,h] ;
X = i , S = [b,d,h,i] ;
no
- c) (za max. 2 body) Definujte predikát prvnivyskyt(?Ceho,+Kde,?Zac,?Kon)
- Predikát uspěje, pokud se prvek
Ceho vyskytuje v seznamuKde .Zac je seznam prvků v seznamu před prvním výskytemCeho ,Kon je seznam prvků za prvním výskytemCeho . - Příklady dotazů a správných odpovědí:
?- prvnivyskyt(c,[a,b,c,d,e,f],[a,b],[d,e,f]).
yes
?- prvnivyskyt(f,[a,b,c,d,e,f],Z,K).
Z = [a, b, c, d, e], K = [];
no
?- prvnivyskyt(c,[a,b,c,c,e,c],[a,b],[c,e,c]).
yes
?- prvnivyskyt(f,[a,b,c,d,e],_,_). % f se v seznamu [a,b,c,d,e] nevyskytuje.
no
?- prvnivyskyt(X,[],_,_). % žádný prvek se v seznamu [] nevyskytuje.
no
?- prvnivyskyt(X,[a,b,c],Z,K).
X = a , Z = [] , K = [b,c] ;
X = b , Z = [a] , K = [c] ;
X = c , Z = [a,b] , K = [] ;
no